How Linear Algebra Powers Computer Science And Ai
As an essential pillar of mathematics, linear algebra equips computer scientists with fundamental tools to solve complex problems. From machine learning to computer graphics, linear algebra enables many critical applications of computing we rely on today.
If you’re short on time, here’s the key point: Linear algebra provides the mathematical foundation for representing and manipulating data in multidimensional space, which allows computers to process data for tasks like machine learning, computer vision, and graphics.
In this comprehensive guide, we’ll explore the indispensable role linear algebra plays across computer science and AI. You’ll learn foundational linear algebra concepts, how they enable multidimensional data analysis, and specific applications powering technologies like self-driving cars, facial recognition, and video games.
Core Concepts in Linear Algebra
Linear algebra is a fundamental branch of mathematics that plays a crucial role in various fields, including computer science and artificial intelligence (AI). Understanding the core concepts of linear algebra is essential for anyone interested in these disciplines.
In this section, we will explore some of the key concepts in linear algebra that power computer science and AI.
Vectors and Vector Spaces
Vectors are mathematical objects that represent both magnitude and direction. In the context of linear algebra, vectors are often used to represent quantities such as position, velocity, and force. They are an essential tool in computer science and AI for representing and manipulating data.
Vector spaces are sets of vectors that satisfy certain properties. They provide a framework for performing operations on vectors, such as addition, subtraction, and scalar multiplication. Vector spaces are fundamental to linear algebra and form the basis for many algorithms and computations in computer science and AI.
Matrices
Matrices are rectangular arrays of numbers or symbols arranged in rows and columns. They are widely used in computer science and AI to represent and manipulate data. Matrices are used to perform operations on vectors, such as rotations, scaling, and transformations.
They are also used in solving systems of linear equations, which is a common problem in computer science and AI.
Matrix Operations
Matrix operations are fundamental to linear algebra and play a vital role in computer science and AI. Some of the key matrix operations include addition, subtraction, multiplication, and transposition. These operations are used to perform computations on matrices and solve various problems.
Eigenvalues and Eigenvectors
Eigenvalues and eigenvectors are important concepts in linear algebra that have applications in computer science and AI. Eigenvalues represent the scalar values associated with a given matrix, while eigenvectors represent the corresponding vectors.
They are used in various algorithms, such as principal component analysis, image compression, and recommendation systems.
Understanding the core concepts in linear algebra, such as vectors, matrices, matrix operations, and eigenvalues/eigenvectors, is essential for anyone working in computer science and AI. These concepts provide the foundation for solving complex problems and developing innovative algorithms.
To learn more about linear algebra and its applications in computer science and AI, you can visit reputable websites such as Khan Academy and Coursera.
Why Linear Algebra Is Critical for Multidimensional Data
Linear algebra plays a crucial role in computer science and artificial intelligence by enabling the representation, manipulation, and analysis of multidimensional data. This branch of mathematics provides powerful tools and techniques that allow researchers and developers to make sense of complex datasets and solve problems in various fields, from image recognition to natural language processing.
Representing Data Points in Space
One of the fundamental concepts in linear algebra is the ability to represent data points in space. In a two-dimensional Cartesian coordinate system, each data point can be represented as a vector with two components: the x-coordinate and the y-coordinate.
However, in real-world applications, data is often much more complex and can have hundreds, or even thousands, of dimensions. Linear algebra allows us to represent these high-dimensional data points as vectors in an n-dimensional space, where each component of the vector represents a different feature or attribute of the data.
This representation is essential for understanding the relationships and patterns within the data.
Transformations and Projections
Linear algebra also enables us to perform transformations and projections on multidimensional data. Transformations involve manipulating the data points using matrices, which can stretch, rotate, or reflect the data in different ways.
These transformations are crucial for tasks like image processing, where resizing, rotating, and applying filters to images require matrix operations. Projections, on the other hand, involve reducing the dimensions of the data while preserving its essential characteristics.
This technique is used in dimensionality reduction algorithms, such as Principal Component Analysis (PCA), which extract the most relevant features from high-dimensional data.
Analyzing Multidimensional Relationships
Another key application of linear algebra in computer science and AI is analyzing the relationships between multidimensional data. Linear algebra provides tools for measuring distances between data points, determining angles between vectors, and calculating similarities or dissimilarities among data points.
These calculations are crucial for tasks like clustering, classification, and recommendation systems. For example, in recommendation systems, linear algebra is used to calculate similarities between users based on their preferences, allowing the system to suggest relevant items or content.
Linear Algebra Applications in Machine Learning
Linear algebra plays a crucial role in various aspects of machine learning, enabling the development and advancement of powerful models and algorithms. Here are some key areas where linear algebra is applied in machine learning:
Implementing Models like Neural Networks
Neural networks, which are widely used in artificial intelligence and machine learning, heavily rely on linear algebra. These models consist of interconnected layers of artificial neurons, and linear algebra provides the mathematical framework for defining and manipulating these connections.
By representing the weights and biases of neurons as vectors and matrices, linear algebra enables efficient computation and optimization of neural network models.
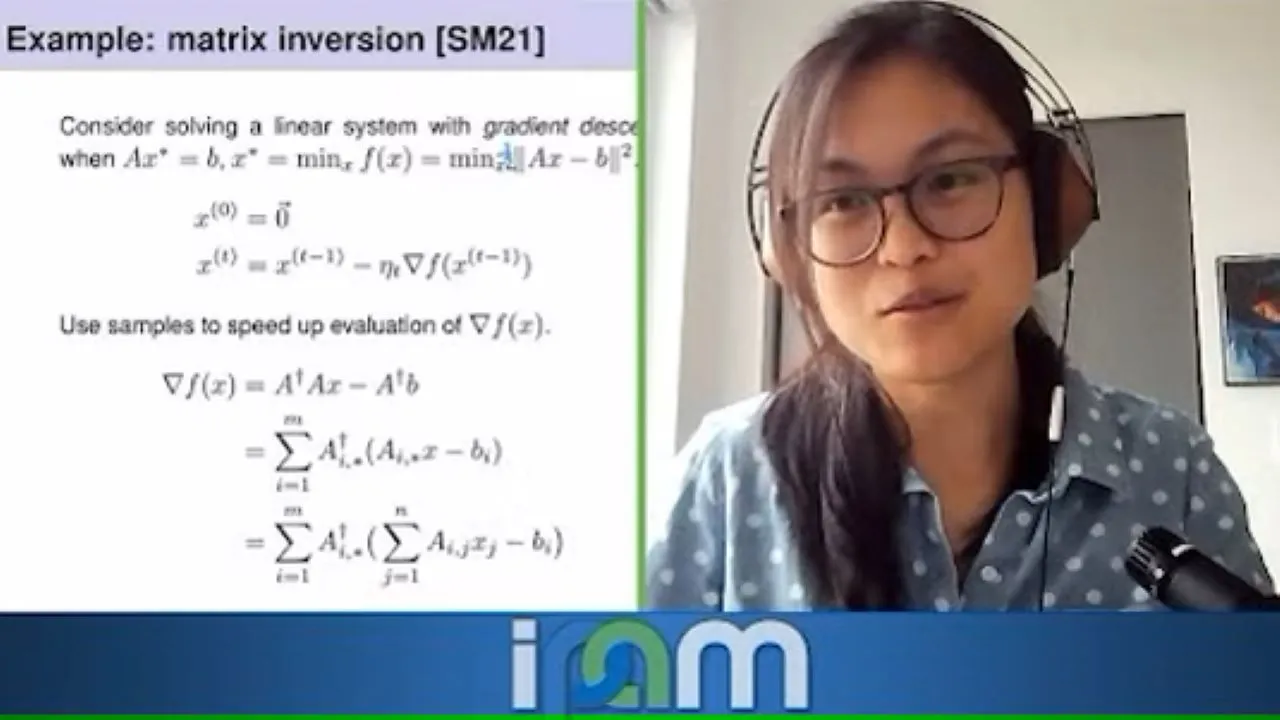
Training Algorithms and Optimization
Linear algebra is also essential in training machine learning algorithms and optimizing their performance. The process of training involves adjusting the parameters of a model to minimize the difference between predicted outputs and actual outputs.
This optimization process often involves solving systems of linear equations or performing matrix factorizations. These techniques help in finding the best set of parameters that lead to accurate predictions.
Improving Predictions through Dimensionality Reduction
Dimensionality reduction techniques are used to reduce the number of features or variables in a dataset while preserving its essential information. Linear algebra provides powerful tools such as singular value decomposition (SVD) and principal component analysis (PCA) for performing dimensionality reduction.
These techniques help in reducing the complexity of machine learning models, improving their efficiency, and avoiding overfitting. By representing data in lower-dimensional spaces, it becomes easier to visualize and understand complex datasets.
Understanding and applying linear algebra concepts in machine learning is crucial for developing sophisticated models, training algorithms, and improving prediction accuracy. By leveraging the power of linear algebra, computer scientists and AI practitioners can push the boundaries of what is possible in the field of machine learning.
Enabling Computer Vision and Graphics
Image Processing and Facial Recognition
Linear algebra plays a crucial role in enabling computer vision and graphics. In the field of image processing, linear algebra is used to manipulate and enhance digital images. Algorithms based on linear algebra are used to perform tasks such as image denoising, image segmentation, and image compression.
Facial recognition, which is widely used in security systems and biometrics, relies heavily on linear algebra algorithms for feature extraction, dimensionality reduction, and classification. These algorithms analyze the facial features and patterns in images or videos, allowing for accurate identification and authentication.
3D Modeling and Rendering
Linear algebra is fundamental to 3D modeling and rendering, which are essential in various industries such as architecture, film production, and game development. In 3D modeling, linear transformations are used to represent the position, orientation, and scale of objects in a virtual 3D space.
This allows for the creation of realistic and interactive 3D environments. Rendering, on the other hand, involves the calculation of lighting and shading effects to generate the final image or animation.
Linear algebra is used to solve complex equations and matrices that describe the interactions between light sources, materials, and surfaces, resulting in visually stunning graphics.
Computer Animations and Video Games
Linear algebra forms the foundation of computer animations and video games. Animation involves the manipulation of objects and characters to create movement and simulate real-world physics. By representing objects as matrices and applying linear transformations, animators can achieve fluid motion and realistic effects.
In video games, linear algebra is used for collision detection, physics simulations, and character movements. Game engines rely on linear algebra algorithms to calculate the positions, velocities, and accelerations of objects in real-time, providing an immersive gaming experience.
Other Key Uses in Computer Science Fields
In addition to its foundational role in areas like machine learning and data analysis, linear algebra plays a vital role in several other computer science fields. Let’s explore some of these key uses:
Cryptography and Cybersecurity
Cryptography, the practice of secure communication, heavily relies on linear algebra concepts. It helps in designing secure encryption algorithms and protocols that protect sensitive information from unauthorized access.
Linear algebra techniques are used to create and solve systems of linear equations, which form the basis of cryptographic algorithms like RSA and AES.
Cybersecurity also benefits from linear algebra’s ability to detect patterns and anomalies in large datasets. By applying linear algebra methods to network traffic analysis, security experts can identify and mitigate potential threats in real-time.
Signal Processing
Signal processing is a field that deals with the analysis, modification, and synthesis of signals. Linear algebra provides the mathematical tools required to analyze and manipulate signals efficiently.
Techniques like Fourier analysis, which decomposes signals into their frequency components, and linear filtering, which removes noise from signals, rely on linear algebra operations.
Linear algebra is widely used in audio and image processing applications. For example, it helps in compressing and decompressing audio and image files, enhancing image quality, and removing unwanted noise from sound recordings.
Recommender Systems
Recommender systems are algorithms that suggest items or content to users based on their interests and preferences. Linear algebra plays a crucial role in building recommender systems by modeling user-item interactions as matrices.
These matrices represent user ratings or preferences for different items.
Using linear algebra techniques like matrix factorization and singular value decomposition, recommender systems can accurately predict user preferences and make personalized recommendations. This has applications in various domains like e-commerce, streaming platforms, and social media.
These are just a few examples of the wide-ranging applications of linear algebra in computer science. Its versatility and power make it an essential tool for solving complex problems and advancing technology in various fields.
Conclusion
Linear algebra empowers computer scientists and data analysts to work effectively in multidimensional vector spaces. Mastering concepts like matrices, transformations, and eigenvalues provides the foundation to tackle machine learning, computer vision, graphics, and many other critical computing applications.
While linear algebra may seem abstract at first, understanding its role in encoding and manipulating complex, high-dimensional data unlocks its immense value within computer science and artificial intelligence.